1. Introduction
State-of-the-art optical technologies are characterized by the highest levels of "precision" possible today. At the same time, the step towards optical applications of tomorrow (e.g. for telescopes, endoscopes, lithography machines or lidar systems) requires the synthesis of know-how of a wide variety of technology fields, such as materials science, optical surface generation, metrology and chemistry as well as mechanical engineering and software development. Consequently, it is essential to develop and apply innovative research methods that are capable of enabling such syntheses [1–4].
Following that trail, the analysis of the morphology of the word re-search itself might be of help. We find it to be a combination of two morphemes: the latin words "re" (meaning "back") and "circare" (meaning "go about"). If we now apply both parts literally and travel back in time to mankind’s origins and start searching there for multi-disciplinary solutions, we find ourselves observing nature herself. Doing so, mankind converted already several solutions from nature into high end technology applications in industry: e.g., gecko’s feet’s van-der-Waals’ contact while walking up walls has been applied to bonding components; chameleon’s gentle grip applied to industrial robots handling delicate parts or, last not least, butterfly’s beautifully colored wings inspiring us to developing diffractive optical elements.
One omnipresent effect in nature is the golden ratio, firstly described by Euclid ago [5]. It describes the shape of nautilus shells, hurricanes and galaxies as well as the hunting pattern of hawks. In general, it seems to be often the golden solution to solve multi-transdisciplinary and complex situations in nature. Therefore, we assume the golden ratio a matter, worthwhile analyzing even from the perspective of leveling-up "precision" towards tomorrows optical technology solutions.
This paper reports on authors first curious steps analyzing the impact of nature’s golden ratio, phi, onto high-end optical systems design.
When we look back at historical times of humankind and if we are interested in optics, our attention is attracted by the time of the renaissance epoch where brilliant and gifted people worked. At that time called "golden age" many thinkers directed their attention to natural and precise sciences. They considered Natural philosophy and science as a single entity. At first we would like to mention Leonardo da Vinci, who was a genius involved at the same time into many activities: i.e. painting, sculpture, architecture, engineering, medicine and fortification. A lot of time Leonardo spent in optical technology, e.g. mirror production. He created special equipment to produce spherical and parabolic concave mirrors. Besides, he discovered illumination phenomena, studied human eye discovering its work, accommodation and converging principles. The first optical equipment for creating artistic canvases was also created by Leonardo da Vinci. Its description can be read in the "treatise on painting"[6], where the author talked about the principle of operation of the optical device. He wrote that the objects displayed on a paper sheet are transmitted not only in their real forms, but also in the same colors. The heritage of Leonardo’s engineering activity is very big, but not all of his inventions were produced. Time-to time somebody tries to reconstruct his inventions, and it works! Leonardo applied the golden ratio in many of his works and paintings, e.g. in the painting "The Annunciation" (Fig. 1.), located in the Uffizi, Florence, Italy. In this paper, we apply the idea of a "golden ratio" to modern lens design.
2. Golden Ratio based Optical Design
In the following, we tested experimentally the possible approach and impact of the use of the golden ratio in optical systems design.
2.1. Single Lens Design
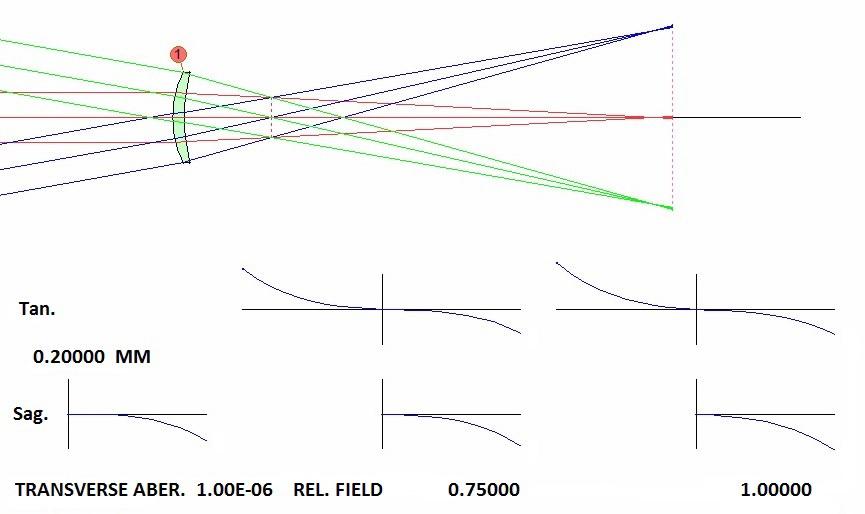
Initially, we have designed a single thin meniscus lens where radii are connected by golden ratio:
R2/R1= 33.87/20.93 = 1.618 (1)
Surface data is presented in Table 1, and system specification in Table 2. Optical scheme is given in Fig. 2. This lens looks well balanced and is free of astigmatism, distortion, see Table 3, and all high order aberrations, see Table 4.
Conclusion: the golden ratio works for this lens design! If radii of a meniscus lens are connected with golden ratio number (1,618), this lens has no astigmatism, distortion or all monochromatic high order aberrations.
Table 1. Surface data:
SURF RADIUS THICKNESS MEDIUM INDEX V-NUMBER
0 INFINITE INFINITE AIR
1 20.92689 2.25000 BK7 1.51679 6166.30 SCHOTT
2 33.87447 17.30000 AIR
3 INFINITE 79.05659S AIR
IMG INFINITE
Table 2. System specification
OBJECT DISTANCE (TH0) INFINITE FOCAL LENGTH (FOCL) 100.0206
OBJECT HEIGHT (YPP0) INFINITE PARAXIAL FOCAL POINT 79.0566
MARG RAY HEIGHT (YMP1) 5.0000 IMAGE DISTANCE (BACK) 79.0566
MARG RAY ANGLE (UMP0) 0.0000 CELL LENGTH (TOTL) 19.5500
CHIEF RAY HEIGHT (YPP1) -4.2776 F/NUMBER (FNUM) 10.0021
CHIEF RAY ANGLE (UPP0) 10.0000 GAUSSIAN IMAGE HT(GIHT) 17.6363
ENTR PUPIL SEMI-APERTURE 5.0000 EXIT PUPIL SEMI-APERTURE 3.9520
ENTR PUPIL LOCATION 24.2597 EXIT PUPIL LOCATION -0.0000
WAVL (uM) .5880000 .5875600 .5860000
WEIGHTS 1.000000 1.000000 1.000000
COLOR ORDER 2 1 3
UNITS MM
APERTURE STOP SURFACE (APS) 3 SEMI-APERTURE 4.03709
FOCAL MODE ON
MAGNIFICATION -1.00021E-10
Table 3. Third-order aberration sums
SPH ABERR COMA TAN ASTIG SAG ASTIG PETZVAL DISTORTION
(SA3) (CO3) (TI3) (SI3) (PETZ) (DI3(FR))
-0.15171 0.05938 -0.04839 -0.04838 -0.04838 0.00625
Table 4. Fifth-order aberration sums
SPH ABERR COMA TAN ASTIG SAG ASTIG PETZVAL DISTORTION
(SA5) (CO5) (TI5) (SI5) (PZ5) (DI5(FR))
-0.00513 0.00376 0.00027 -2.275E-05 -9.499E-05 -1.403E-05
2.2. Double Lens Design
Subsequently, the same idea has been applied for a dual meniscus lens design presented in Fig. 3. The calculation for radii, thicknesses and distances between the two lenses was carried out as follows:
We start from single thin meniscus where R1 and R2 are connected with golden ratio, see equation (1).
Add second meniscus lens located right from the aperture stop located on surface 3.
Calculate R3=-R2/1.618=-20.936 mm
Calculate R4=-R1/1.618=-12.934 mm
Calculate second lens thickness: d4=d1x0.618=1.39 mm;
Calculate distance between aperture stop to the second lens: d3=d2x0.618=10.69 mm
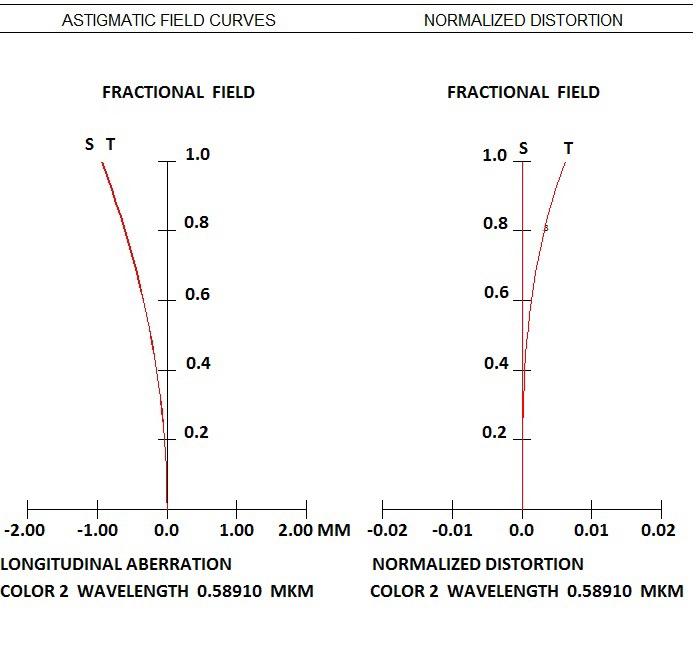
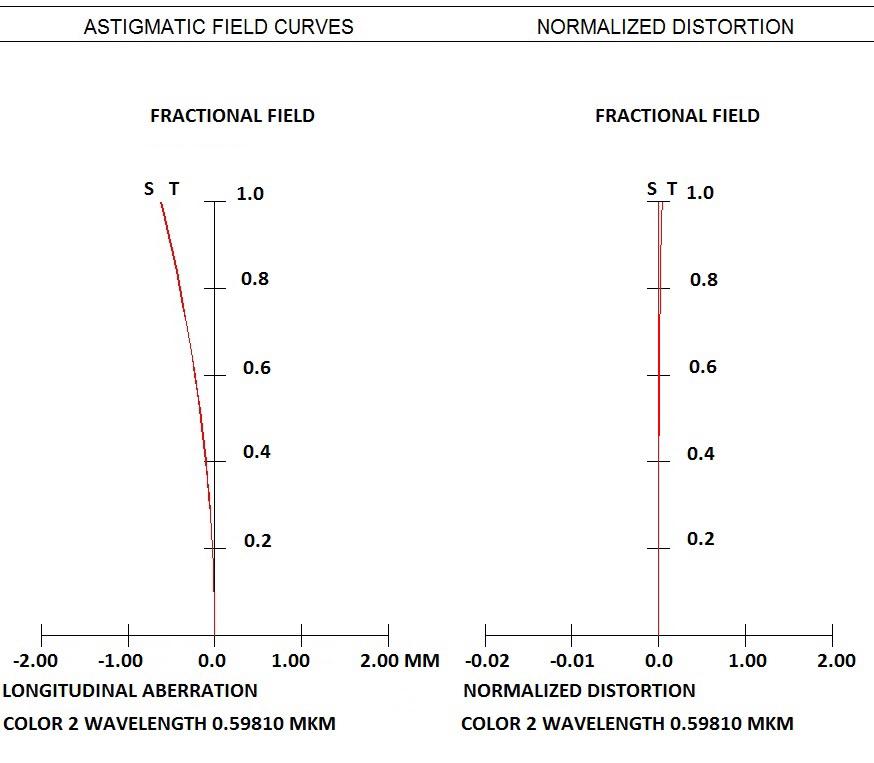
Conclusion: Golden ratio works for this design also! This lens has no astigmatism, distortion and all monochromatic high order aberrations are close to zero: see table 5-8 and Fig.4, where plots of residual astigmatism and distortion are presented.
Table 5. System specification data
OBJECT DISTANCE (TH0) INFINITE FOCAL LENGTH (FOCL) 49.0290
OBJECT HEIGHT (YPP0) INFINITE PARAXIAL FOCAL POINT 32.9142
MARG RAY HEIGHT (YMP1) 5.0000 IMAGE DISTANCE (BACK) 32.9142
MARG RAY ANGLE (UMP0) 0.0000 CELL LENGTH (TOTL) 33.4405
CHIEF RAY HEIGHT (YPP1) -4.2776 F/NUMBER (FNUM) 4.9029
CHIEF RAY ANGLE (UPP0) 10.0000 GAUSSIAN IMAGE HT(GIHT) 8.6451
ENTR PUPIL SEMI-APERTURE 5.0000 EXIT PUPIL SEMI-APERTURE 5.1921
ENTR PUPIL LOCATION 24.2597 EXIT PUPIL LOCATION -17.9983
WAVL (uM) .5880000 .5875600 .5860000
WEIGHTS 1.000000 1.000000 1.000000
COLOR ORDER 2 1 3
UNITS MM
APERTURE STOP SURFACE (APS) 3 SEMI-APERTURE 4.03709
FOCAL MODE ON
Table 6. Surface data
SURF RADIUS THICKNESS MEDIUM INDEX
0 INFINITE INFINITE AIR
1 20.92689T 2.25000T BK7 1.51679T SCHOTT
2 33.87447T 17.30000 AIR
3 INFINITE 10.70000 AIR
4 -20.93601P 1.39050P BK7 1.51679P
5 -12.93380P 32.91422S AIR
IMG INFINITE
Table 7. Third-order aberration summs
SPH ABERR COMA TAN ASTIG SAG ASTIG PETZVAL DISTORTION
(SA3) (CO3) (TI3) (SI3) (PETZ) (DI3(FR)
-0.27821 -0.16727 -0.06211 -0.06209 -0.06209 0.00043
Table 8. Fifth-order aberration summs
SPH ABERR COMA TAN ASTIG SAG ASTIG PETZVAL DISTORTION
(SA5) (CO5) (TI5) (SI5) (PZ5) (DI5(FR))
-0.01998 -0.00951 -0.00028 0.00020 0.00032 -3.255E-05
3. Conclusion
In nature, beauty is often to be equivalent with being strong in survival skills, reproduction and protection. The perception of beauty herself can be found in the golden ratio, which mathematically describes human’s evolutionary perception of the "best solution" while interacting as a being within nature. Therefore, we might define our inclination towards beauty as an evolutionary "optimization method generated by nature". This paper demonstrated that it is worthwhile going back in time, challenging modern methodology of research methods by analyzing solutions generated by nature herself. First steps along this trail have been made experimentally and promising insights have been generated applying the "golden ratio approach" to State-of-the-Art optical systems design. Although the golden ratio approach to optical design reported in this paper generated impressive preliminary results, we must of course take into account that all “optimization techniques” installed by nature do not contain the claim to absoluteness but to evolutionary trial and error survival of the best. The golden ratio approach is in authors’ conviction a perfect complementary method to the application of modern high technology software tools based on Snellius law, only. Therefore, it is true, that by analyzing the past we gain insights that might help us to design an optimum future; even in optics technologies. The idea of the authors was continued. The Swiss company Fishba became interested in its application in production, and the results of joint research of scientists and business representatives were presented in a report in September 2021 at the EOS conference on ultrafast optical technologies and applications, Rome, Italy (13-17 September 2021, EOS meeting on Ultrafast optical technologies and applications, Rome, Italy).
Лившиц, И. Л. Леонардо да Винчи и современная оптика. Возможности применения принципа "золотого сечения" к оптическому дизайну/ Волкова, С. Л., Лившиц, И. Л., Толстикова, И.И., Фэнле, О. // Культура и технологии. 2022. Том 7. Вып. 4. С. 144-150. DOI: 10.17586/2587-800X-2022-7-4-144-150
- Östlund, U., Kidd, L., Wengström,Y., Rowa-Dewar, N. (2011). Combining qualitative and quantitative research within mixed method research designs: A methodological review. International Journal of Nursing Studies. Vol. 48. 369-383. Iss. 3. DOI: 10.1016/j.ijnurstu.2010.10.005.
- Williams, C. (2007). Research Methods. Journal of Business & Economics Research (JBER). Vol. 5. No. 3. 65-72. DOI: 10.19030/jber.v5i3.2532.
- Faehnle, O. (2016). Process optimization in optical fabrication. SPIE Journal on Optical Engineering. Vol. 55. No. 3. 035106. DOI: 10.1117/1.OE.55.3.035106.
- Zare Mehrjerdi Y. (2011). Six‐Sigma: methodology, tools and its future. Assembly Automation. Vol. 31. No. 1. 79-88. DOI: 10.1108/01445151111104209.
- Euclid. Sketch and explanation of the golden ratio. Book 2. Proposition 5.Oxyrhynchus Papyri, Egypt (28°32′N 30°40′E); ca. 100 AD.
- Melzi, F. (1632). Leonardo da Vinci’s “Treatise on Painting”. France.
- Livshits, I., Faehnle, O. (2020). Producibility analysis of a lens system during the optical design stage. Scientific and Technical Journal of Information Technologies, Mechanics and Optics. Vol. 20. No. 5. 625-633. DOI: 10.17586/2226-1494-2020-20-5-625-633.
- Tinner, M., Faehnle, O., Livshits, I. (2020). PanDao fabrication cost impact analysis software tool for optical designers. EPJ Web of Conferences. Vol. 238. 03014. DOI: 10.1051/epjconf/202023803014.